Livro didático 2 da disciplina
Olá,
Seja bem-vindo ao tópico 2 da nossa disciplina. Aqui você vai estudar:
- Noções de lógica matemática
- Relações
- Funções
- Classificação de funções
| Site: | Moodle - IFSC |
| Course: | 20.1 - Tópicos de Matemática Elementar |
| Book: | Livro didático 2 da disciplina |
| Printed by: | Usuário visitante |
| Date: | Monday, 15 September 2025, 10:20 PM |
1. Apresentação tópico 2
Seja bem-vindo ao livro virtual 2 da nossa disciplina, aqui o roteiro de estudos é voltado aos temas que abrangem a Unidade Curricular 2, assim como terá acesso ao conjunto de materiais em pdf, cuja leitura é obrigatória para a compreensão do conteúdo.
Os conteúdos do tópico 2 são:
- Noções de lógica matemática
- Relações
- Funções
Os materiais aqui apresentados são autoria/adaptação de:
GIMENEZ, Carmen S. C., STARKE, Rubens. Introdução ao Cálculo 2. ed. – Florianópolis : UFSC/EAD/CED/CFM, 2010. 261p.
IEZZI, G.; MURAKAMI, C. Fundamentos de matemática elementar: conjuntos e funções. São Paulo: Atual, 2013. v. 1.
Lembre-se
Não se esqueça de fazer os exercícios e tarefas que estão listados ao longo de cada capítulo, no próprio material, para sua fixação e aprofundamento dos conteúdos estudados.
2. Noções de lógica matemática
Além de servir largamente à computação, os elementos de lógica matemática norteiam todo o raciocínio dedutivo matemático, no sentido de demonstrar, formal e cabalmente, os resultados que precisamos e procuramos para explicar o maior número possível de elementos lógicos e abstratos através da linguagem matemática.
Com isto, é muito importante entender o que exatamente são as proposições e seus derivados, pois são estas proposições que permitirão (e você vai compreender isto com o tempo) avançar com o conhecimento matemático epistemologicamente falando.
Enunciaremos, ao longo do curso, muitas implicações e equivalências matemáticas. Mas o que exatamente são estes dois elementos? Clicando no endereço fonte da imagem, você aprenderá uma maneira de gravar esta tabela verdade padrão.
Neste primeiro capítulo, você vai estudar:
- proposições (definição, exemplos e valores lógicos);
- conectivos (composição de proposições);
- implicação e equivalência lógica
- negações lógicas
- quantificadores lógicos.
Leitura obrigatória
Clique aqui para ler o material sobre lógica matemática.
Acompanhe o vídeo que mostra um pouco mais sobre a lógica e sua importância na matemática.
Em seguida, veja o vídeo que mostra como se construir tabelas verdade.
Continuando, o próximo vídeo fala de negações lógicas. Vamos utilizar muito delas na matemática!
3. Relações binárias
O conceito de relações é o precursor necessário do estudo das funções. Uma vez estudado o que vem a ser o produto cartesiano entre dois conjuntos A x B (nesta
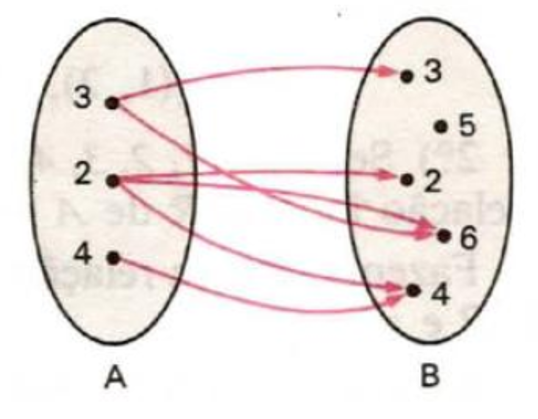
ordem!), podemos então definir o que vem ser relações binárias.
Muitos exemplos dessas relações conduzem-nos às mais diversas formas de funções, que serão visualizadas gráfica e algebricamente. Compreender o conceito de domínio, contradomínio e imagem aqui é essencial para que, em muitas oportunidades no futuro, possamos estudar diversos tipos de funções, cujos conjuntos envolvidos terão elementos que, no momento, sequer imaginamos.
Fonte: IEZZI, G. MURAKAMI, C.: Fundamentos de Matemática Elementar, vol. 1, 7 edição, Editora Atual
A Geometria Analítica, que será estudada no terceiro semestre, vai nos trazer muito mais exemplos de relações e suas representações no plano cartesiano. Serão equações e inequações de retas, circunferências, semiplanos, regiões do plano, curvas cônicas, etc. Dali em diante, este fundamental conceito matemático jamais vai nos abandonar em nosso estudo.
Neste segundo capítulo, você vai estudar:
- relações (definição e exemplos);
- propriedades das relações (reflexividade, simetria e transitividade);
- relação de equivalência (aquelas que são reflexivas, simétricas e transitivas ao mesmo tempo);
- relação de ordem(aquelas que são reflexivas, antissimétricas e transitivas ao mesmo tempo);
- relações em R × R (ou relações no plano cartesiano).
Vamos então à leitura do conteúdo.
Após a leitura obrigatória assista ao vídeo e observe na prática como ensinar as relações binárias.
Na prática
Assista a aula e veja na prática como ocorrem as relações binárias.
4. Funções
As funções consistem, via de regra, no conteúdo de todo o primeiro ano do Ensino Médio, considerando que, para aqueles que forem ingressar em algum curso superior que envolva diretamente as ciências chamadas de exatas, este tema é a base fundamental e necessária para o estudo das sofisticadas ferramentas do cálculo e álgebra, necessárias para o trabalho de profissionais como os das engenharias.
Além disso, os diversos tipos de funções (polinomiais, exponenciais e logarítmicas, trigonométricas, entre outras) são muito importantes como modelos matemáticos dos mais diversos temas de estudo da ciência. Esses tipos de funções serão objeto de estudo no tópico 3 a seguir.
O tema do capítulo anterior (relações), por sua vez, é o precursor necessário para o entendimento matemático do conceito de funções. Uma vez que entendemos o que é uma função, este ente vai continuar conosco durante toda nossa formação como matemáticos, ou professores de matemática.
A matemática moderna constrói-se totalmente alicerçada nos conceitos de conjunto e... funções!! Veja a seguir alguns exemplos. Durante o curso, você vai descobrir muitos, muitos outros tipos de funções.
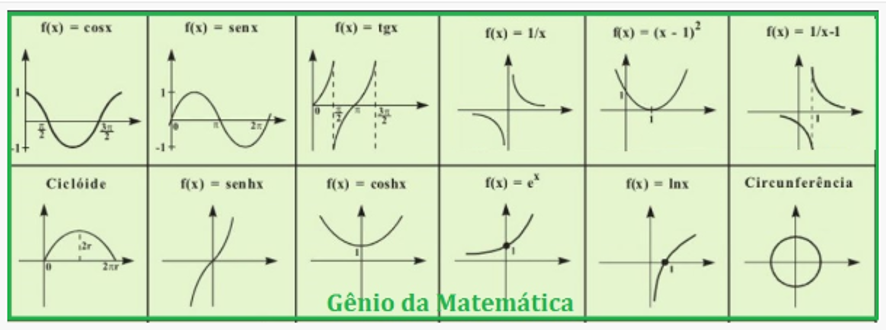
Fonte: http://geniodamatematica.com.br/formulas-de-matematica/
Na figura anterior, alguns exemplos de gráficos (nem todos de funções) que mostram um pouco do vasto universo em que vamos, definitivamente, adentrar agora.
Neste terceiro capítulo, você vai estudar:
- funções (definição formal);
- gráfico de funções;
- classificação de funções (funções crescentes, decrescentes, sobrejetoras, injetoras e bijetoras);
- composição de funções ("funções de funções");
- funções inversas (relações inversas que também consitituem funções).
Vamos portanto, ao estudo deste importante conteúdo.
Leitura obrigatória
Clique aqui para ler o material sobre funções.
Após a leitura obrigatória assista ao vídeo e observe na prática como aplicar as funções
Na prática
Assista a aula e veja na prática como as funções podem ser apresentadas.

