Aplicação de REDS no Ensino da Matemática
Livro de leitura obrigatória da Unidade de Estudos 2.
| Site: | Moodle - IFSC |
| Curso: | 22.1 - Laboratório de Matemática |
| Livro: | Aplicação de REDS no Ensino da Matemática |
| Impresso por: | Usuário visitante |
| Data: | terça, 16 Set 2025, 01:37 |
1. Os Dados do Processo de Ensino-aprendizagem da Matemática no Brasil

Os Dados do Processo de Ensino-aprendizagem da Matemática no Brasil
Para tratar deste tema, especialmente relevante em um Curso de Licenciatura de Matemática, utilizar-se-á da Dissertação de Mestrado de Maia (2021), utilizando-se, para tanto, de trechos extraídos na íntegra, desde a página 18 até a página 20, conforme segue:
Queixas quanto ao ensino e à aprendizagem da Matemática são constantes na Educação Básica. Entre professores e alunos, é possível constatar reclamações acerca da apreensão de conteúdos e conceitos matemáticos. Esta disciplina tem sido, quase sempre, responsável pelos mais baixos níveis de rendimento escolar. As disciplinas relacionadas à área são vistas como barreiras durante a vida estudantil, o que pode comprometer a formação do cidadão, pois a Matemática faz parte da vida cotidiana, sendo, inclusive, uma das formas de linguagem da sociedade.
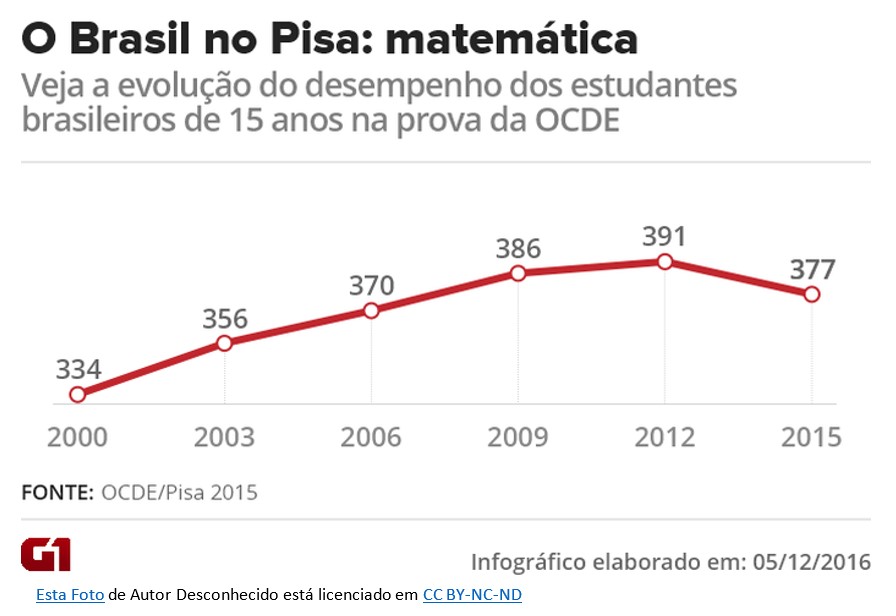
Dados do Programa Internacional de Avaliação de Estudantes (PISA 1) reafirmam esse perfil, no que tange à aprendizagem dos conceitos matemáticos pelos discentes brasileiros. Considerando as três competências avaliadas – Leitura, Ciências e Matemática – nesta última, os brasileiros apresentam a menor média2. Embora o Brasil tenha avançado do índice de 356 pontos em 2003, para 370 em 2006 e 386 pontos em 2009, continua, de forma significativa, abaixo da média dos demais países membros da Organização para a Cooperação e Desenvolvimento Econômico (OCDE). De acordo com os dados da última edição do PISA, a média geral foi de 496 pontos (OCDE, 2010). O Brasil tem crescido, em média, 15 pontos por triênio, mas encontra-se abaixo da média 110 pontos. Dentre os 65 países e economias 3 que participaram da última avaliação, o Brasil ocupa o 57º lugar na proficiência em Matemática.
Abaixo, o gráfico demonstra melhor tais dados:
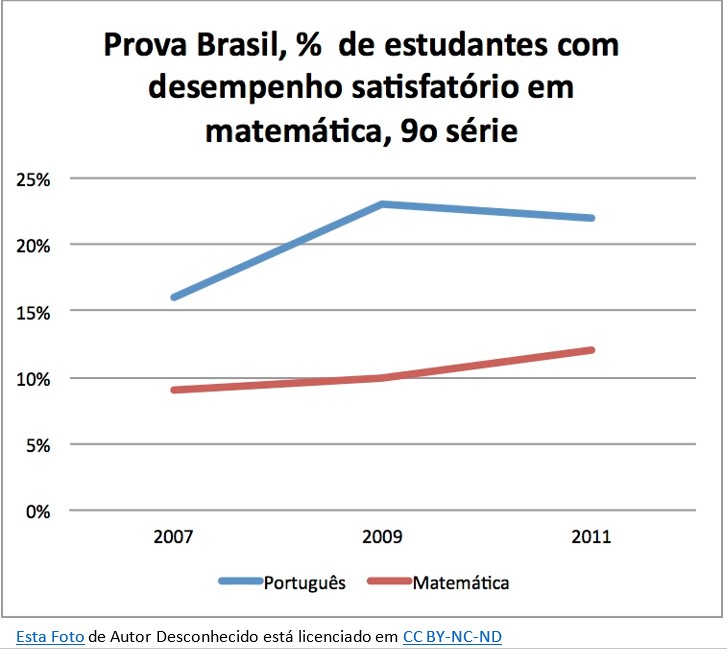
Em nível nacional dados do Sistema de Avaliação da Educação Básica (SAEB 4) demonstram panorama semelhante. Conforme resultados do último estudo disponível, realizado em 2009, a média nacional de proficiência em Matemática dos alunos do 5º ano do Ensino Fundamental atingiu a marca de 199,52 pontos. Embora essa pontuação signifique um avanço em relação aos 193,48 pontos alcançados em 2007, em ambos os casos os alunos não atingiram a pontuação mínima satisfatória, indicada pelo Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (INEP) para aquela faixa de escolaridade. Para o referido Instituto, o índice mínimo para aquele grupo de alunos é de 200 pontos, que ainda os deixa no nível 3, conforme a escala de proficiência do SAEB.
Abaixo, o gráfico demonstra melhor tais dados:
Esse baixo desempenho indica que os alunos têm poucas experiências em resolução de problemas, o que compromete aspectos como desenvolvimento da capacidades de observação, estabelecimento de relações, comunicação com uso de diferentes linguagens, argumentação e validação de processo. Disso depreende-se que as práticas educativas em Matemática demandam novas estratégias pedagógicas que possibilitem ao alunos o desenvolvimento daquelas competências.
Perez (1999, p. 268) afirma que é necessário valorizar a criatividade discente nas aulas de Matemática, “com atividades ambíguas, complexas, com desafios, fazendo com que os estudantes se tornem sensíveis aos estímulos do ambiente, sejam capazes de adaptar-se a mudanças e consigam resolver problemas não convencionais”. A Matemática mostra-se uma boa solução para estimular formas de raciocínio como intuição, indução, dedução e estimativa, portanto contribui para o desenvolvimento cognitivo dos estudantes. Nos PCN, a Matemática é vista como “um componente importante na construção da cidadania, na medida em que a sociedade se utiliza, cada vez mais, de conhecimentos científicos e recursos tecnológicos, dos quais os cidadãos devem se apropriar” (BRASIL, 1997b, p. 19).
Tais reflexões sobre o ensino da Matemática devem ser frequentes nos currículos escolares para evitar procedimentos mecânicos. No entanto, parecem não chegar à sala de aula. O ensino de Matemática, em muitos casos, tem se restringido ao uso de regras mecânicas, limitando-se à aplicação de fórmulas e à memorização de elementos básicos, sem a compreensão de conceitos nem o estabelecimento de relações entre a Matemática da escola e a Matemática da vida. Para D'Ambrósio (1989) isso ocorre devido a uma compreensão errada que alguns professores têm de que ensinar bem Matemática é passar o máximo de conteúdos através de um maior número possível de exercícios. Esses dados indicam que o problema da aprendizagem matemática, dentre outros fatores, também estaria fortemente ligado à prática docente.
Diante desses problemas, expectativas de melhoria voltam-se para pesquisas e novas práticas pedagógicas baseadas em teorias capazes de propiciar a superação das dificuldades. Nesse contexto, estão as tendências presentes na Educação Matemática, como forma de contribuir para a preparação docente e para o trabalho com a disciplina na escola. Dentre elas, destaca-se o uso da Informática Educativa apontada como uma das tendências mais difundidas. De acordo com Mendes (2009), o uso de computadores no ensino da Matemática contribui para que discentes e docentes superem alguns obstáculos no processo de ensino-aprendizagem.
Questões pertinentes ao contato dos alunos com as tecnologias digitais são relevantes. Há, todavia, que se atentar para a formação do professor, responsável por possibilitar essa experiência, com vistas a uma aprendizagem significativa e à construção de novos conhecimentos pelo aprendiz. Seja qual for o recurso pedagógico, ele só será bem empregado quando o professor souber tirar melhor proveito do potencial didático-pedagógico do artefato. Faz-se necessário que os professores reconheçam tais ferramentas como instrumentos de ensino capazes de contribuir para sua prática docente e, por conseguinte, para a aprendizagem discente. Importa que os professores construam conhecimentos que lhes tornem aptos a apontar possibilidades e limitações das tecnologias.
1 Programee for International Student Assessment. Trata-se de um programa internacional de avaliação comparada, cuja principal finalidade é produzir indicadores sobre a efetividade dos sistemas educacionais, avaliando o desempenho de alunos na faixa etária dos 15 anos de idade em que se pressupõe o término da escolaridade básica obrigatória na maioria dos países. Esse programa é desenvolvido e coordenado internacionalmente pela OCDE, havendo em cada país participante uma coordenação nacional, que, no Brasil, cabe ao Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (BRASIL, 2010).
2 No último estudo disponível, referente à avaliação de 2009, o Brasil apresentou média de 412 pontos de proficiência em Leitura e 405 pontos em Ciências.
3 Nesse estudo, alguns países são desmembrados em função de sua economia como é o caso da Índia (Himachal Pradesh, Tamil Nadu), China (Hong Kong e Macau), Venezuela (Miranda) e Holanda (Antilhas).
4 De acordo com a Portaria Nº 931, de 21 de março de 2005, o SAEB é composto por dois processos: a Avaliação Nacional da Educação Básica (ANEB) e a Avaliação Nacional do Rendimento Escolar (ANRESC), mais conhecida como Prova Brasil (BRASIL, 2010).
2. Tecnologias digitais e Educação Matemática
Tecnologias digitais e Educação Matemática
De acordo com Ponte apud Lealdino Filho (2013), o ensino da Matemática apresenta alguns aspectos problemáticos:
A reflexão sobre os aspectos problemáticos do ensino de matemática evidencia vários fatores que colocam a disciplina como um item não atrativo e incômodo do currículo da educação básica. A matéria geralmente é tida como algo extremamente difícil que lida com objetos e teorias fortemente abstratas, mais ou menos incompreensíveis (LEALDINO FILHO, 2013, p. 17).
Segundo Reis (2000), as principais causas para rejeição à matemática são:
- a falta de motivação do professor ao ensinar e falta de motivação dos alunos em aprender;
- a ideia pré-concebida e aceita pelos alunos de que a matemática é difícil;
- o rigor da matemática;
- experiências negativas que os alunos tiveram com a matéria;
- falta de relação entre a matéria ensinada na escola e o cotidiano do aluno;
- a prática do professor, as relações que este estabelece com os alunos e a forma com que ensina e avalia.
Destes elementos depreende-se que o professor é o principal elemento para a mudança quanto a rejeição à matemática. O professor pode, então, tomar algumas medidas (TATTO; SCAPIN, 2004):
- fazer uma reflexão e uma auto avaliação da prática pedagógica;
- conhecer a realidade social do aluno;
- conhecer como acontece o desenvolvimento cognitivo do aluno para não reforçar experiências negativas quanto a matemática;
- adequar materiais e recursos metodológicos;
- estabelecer conexões entre o conhecimento matemático e sua aplicabilidade em situações reais.
A utilização dos REDs, especialmente dos jogos matemáticos, podem ser muito úteis para o alcance da motivação dos alunos na aprendizagem da matemática. Como aponta-nos Maia (2012, p. 47-48):
A característica multimídia das tecnologias digitais traz um potencial para a geração de novas estratégias didáticas para a educação. Nas práticas de ensino e de aprendizagem, a Informática Educativa pode ser utilizada como um auxílio às aulas, tornando-as mais atraentes e em sintonia com o aprendizado paralelo e multitarefa das crianças (VRAKKING; VEEN, 2008). Porém, mais que isso, as tecnologias digitais podem proporcionar a alunos e professores um universo de informações úteis e de perspectivas diferentes de percepção de um mesmo conceito, oferecendo assim, condições favoráveis ao aprendizado. M. Silva (2009) ressalta que o uso de softwares educativos e educacionais, por exemplo, tem contribuído para a educação escolar em diferentes dimensões, seja pelo aspecto social, com a promoção da inclusão digital, ou pela vertente cognitiva. Uma vez que diversificam as atividades pedagógicas, tais recursos concorrem para a melhoria da aprendizagem discente.
Ao utilizar recursos desta natureza, o professor de matemática poderá trabalhar em prol da participação dos alunos no processo de ensino-aprendizagem, construindo um outro modelo de aula, mais ativo e participativo por parte dos estudantes, ao invés de uma aula somente em um formato chamado de 'tradicional'.
Essa denominação reúne características como a aula em forma de monólogo, a repetição exaustiva de exercícios, a memorização de algoritmos e a baixa exploração de habilidades cognitivas de ordem mais elevada como raciocínio lógico e emprego de heurísticas. [...] A participação ativa dos alunos se reveste de uma importância particular. Obter a atenção e engajamento da classe é de importância capital para melhorar a eficiência do processo de ensino, ampliar a compreensão e aumentar os índices de retenção de conhecimento (LEALDINO FILHO, 2013, p. 22).
Assim, quando tratamos desses estilos de aula, estamos falando de tipos de abordagem pedagógica.
Seymour Papert (1994), ao discutir o uso de computadores para a educação, cunhou duas expressões para distinguir dois tipos de abordagem pedagógica da máquina, quais sejam: instrucionista e construcionista. A primeira tem base epistemológica behaviorista, em que o computador assume o papel de máquina de ensinar. Nessa concepção, a aprendizagem significa memorização dos conteúdos (VALENTE, 1999). As máquinas de ensinar de B. F. Skinner, expoente dessa abordagem pedagógica foram projetadas a partir dessa concepção de aprendizagem e fundamentaram diversos métodos de ensino e recursos pedagógicos.
A abordagem pedagógica construcionista para o uso de computadores em educação tem cunho cognitivista. Baseada nas ideias de Piaget e Vygotsky, a máquina é vista como uma ferramenta que estimula o pensamento e a criação. Papert (1994), criador de tal abordagem, afirma que práticas educativas com computadores podem ser mais produtivas quando trabalhadas dentro da abordagem construcionista. Essa perspectiva da Informática Educativa centra-se no desafio, no conflito e na descoberta o que torna a aprendizagem mais significativa para o aluno.
No construcionismo, o controle do processo de aprendizagem fica nas mãos do educando ou este o compartilha com a máquina (VALENTE, 1999). Ao professor são oferecidas “maiores chances de compreender o processo mental do aluno, ajudá-lo a interpretar as respostas, questioná-lo, colocar desafios que possam ajudá-lo na compreensão do problema e conduzi-lo a um novo patamar de desenvolvimento” (ALMEIDA, 2000, p. 20). Nessa perspectiva, o professor deixa de ser mero transmissor de conteúdos e transforma-se em um facilitador da aprendizagem, proporcionando ao aluno o desenvolvimento intelectual e criativo (MAIA, 2012, p. 48).
Para uma aula fundamentada em uma abordagem construtivista, o professor deve:
D'Ambrósio (1989, p. 5) afirma que o ensino de Matemática através da Informática Educativa, baseada na abordagem pedagógica construcionista, "tem o poder de dar ao aluno a autoconfiança na sua capacidade de criar e fazer matemática. Com essa abordagem a Matemática deixa de ser um corpo de conhecimentos prontos e simplesmente transmitidos aos alunos e passa a ser algo em que o aluno faz parte integrante no processo de construção de seus conceitos".
O uso de computadores no ensino da Matemática desvela vantagens tanto para o ensino, entendidas como as ações mais diretamente ligadas ao professor, como para a aprendizagem desenvolvida pelo aluno (BITTAR, 2010). A associação entre a informática e a Educação Matemática pode proporcionar mudanças significativas para a prática educativa também é assinalada por Borba e Penteado (2010).
Segundo Bittar (2010, p. 593) algumas pesquisas, que relacionam tecnologias digitais e o ensino da Matemática, “têm mostrado que o uso adequado de um software pode permitir melhor apreensão do conceito pelo aluno”. Gladcheff, Zuffi e Silva (2001, p. 2) apontam que o computador nas aulas de Matemática do Ensino Fundamental pode ser “considerado um grande aliado do desenvolvimento cognitivo dos alunos, principalmente na medida em que possibilita o desenvolvimento de um trabalho que se adapta a distintos ritmos de aprendizagem e favorece que o aluno aprenda com seus erros”.
Convém registrar que essas condições proporcionadas pelo uso de tecnologias digitais na educação são propícias para que o professor desenvolva situações didáticas no ensino de Matemática, como propõe Brousseau (1996). A Informática Educativa nas aulas de Matemática favorece a aprendizagem a partir da resolução de problemas apresentados pelo professor ao aluno, a fim de que ele interaja com o meio e com outros indivíduos. Essas experiências de resolução de problemas podem ser vivenciadas pelos alunos sem que percebam que estão de fato aprendendo. Através desse tipo de atividade, os aprendizes constroem esquemas mentais que poderão ser utilizados em outras situações semelhantes (MAIA, 2012, p. 49-50).
Ao descrever os passos de trabalho do professor de Matemática, Brousseau (1996) propõe que o trabalho do professor deve consistir em:
I) propor situações de aprendizagem para o aluno;
II) provocar a elaboração das respostas;
III) fazer funcionar as situações e modificá-las (MAIA, 2012, p. 49).
3. Uso de Jogos e Construção de Jogos
Uso de Jogos já Existentes
São inúmeros os recursos disponíveis, como objetos de aprendizagem e softwares educativos, que podem auxiliar na construção de conhecimentos matemáticos. Essas características da Informática Educativa nas aulas de Matemática promovem o desenvolvimento da autonomia dos usuários, discentes e docentes, pois instigam os sujeitos a pensar, refletir e criar soluções para os problemas apresentados ou demandados. Essa prática pode, inclusive, mobilizar conteúdos atitudinais, como indicam os PCN, promovendo o desenvolvimento da autoconfiança para resolver problemas matemáticos (MAIA, 2012, p. 51-53.
Tais fatos corroboram o posicionamento de Mendes (2009, p. 113) que afirma: “a informática, atualmente, é considerada uma das componentes mais importantes para a efetivação da aprendizagem matemática no mundo moderno”.
D'Ambrósio (apud PEREZ, 1999) compreende que o uso das tecnologias digitais deve ser um dos papéis que o professor de Matemática deve assumir na atualidade. Tais posicionamentos parecem justificar o fato de a Informática Educativa e suas variáveis28 figurarem entre as tendências da Educação Matemática, tanto do ponto de vista metodológico (MENDES, 2009), quanto investigativo (PEREZ, 1999; FIORENTINI; LORENZATO, 2006) (MAIA, 2012, p. 51-53).
Muitas opções de REDs para o ensino da matemática já foram apresentas no capítulo de estudos 1, desta unidade curricular.
Especificamente em relação ao elemento "JOGO", vale ressaltar que ö jogo é um grande aliado, para não dizer o melhor, do desenvolvimento cognitivo das crianças". (AGUILÁ, 2014, p. 11). Sobre este aspecto, o mesmo autor continua suas colaborações, afirmando:
É imprescindível para o amadurecimento das estruturas mentais, que incluem processos como percepção, memória, atenção, domínio da linguagem ou a estruturação do pensamento. O jogo foi, é e sempre será uma das ferramentas mais eficientes para promover o aprendizado e construir o conhecimento graças ä sua capacidade de simular a realidade, oferecendo um cenário seguro para cometer erros e aprender com eles na prática.
Nesse sentido, as principais capacidades cognitivas estimuladas pelo jogo são:
- capacidade de compreensão
- capacidade crítica
- capacidade criativa
- capacidade complexa
Aguilá (2014), propõe que os jogos podem ser divididos em:
- Jogos de cálculo matemático e inteligência numérica
- Jogos de capacidade e raciocínio lógicos e agilidade mental
- Jogos de estratégia e paciência
- Jogos de memória e observação
- Jogos de inteligência e raciocínio verbais e de comunicação
- Jogos de raciocínio e enigmas
Jogo retirado da obra "Jogos para aguçar a inteligência - 111 enigmas surpreendentes e muito divertidos", de Jorge Batllori Aquilá.
Construção de Jogos
Para além de recursos prontos, o próprio professor pode construir os jogos e recursos que pretende usar. No entanto, alguns cuidados precisam ser tomados.
A concepção de um jogo educacional, incluindo os conteúdos abordados e a mecânica do mesmo, não é uma atividade determinística. Assim como preparar uma sequência didática interessante e efetiva requer de um professor experiência e uma dose de criatividade, o desenvolvimento de um jogo educacional também envolve um esforço de concepção livre. Dois subterfúgios para auxiliar essa fase consistem em definir mapeamentos entre operações que se deseja ensinar e operações existentes em jogos; e explorar um leque de opções, como diferentes cenários e gêneros (ação, puzzle, RPG, etc.) antes de definir a implementação definitiva (KOSCIANSKI apud LEALDINO FILHO, 2013, p. 27-28).
Algumas opções de plataformas digitais para construção de jogos são:
1. Kahoot! - plataforma de aprendizado baseada em jogos, usada como tecnologia educacional em escolas e outras instituições de ensino. Seus jogos de aprendizado, "Kahoots", são testes de múltipla escolha que permitem a geração de usuários e podem ser acessados por meio de um navegador da Web ou do aplicativo Kahoot.
2. Geogebra - GeoGebra é um software de matemática dinâmica para todos os níveis de ensino que reúne geometria, álgebra, folhas de cálculo, gráficos, estatística e cálculo numa aplicação fácil de utilizar. GeoGebra é uma comunidade em rápida expansão de milhões de utilizadores localizados em praticamente todos os países. GeoGebra tornou-se líder no fornecimento de software de matemática dinâmica, apoiando a ciência, tecnologia, engenharia e matemática (STEM) educação e inovações no ensino e aprendizagem em todo o mundo.
3. Jamboard - é uma ferramenta Google; é um quadro branco inteligente que se conecta ao ecossistema do buscador, para interação com aplicativos. Pode ser usado para jogos.
Fazendo uma busca simples, é possível localizar tutoriais para aprender como usar cada um desses recursos.
Abaixo, segue um tutorial de criação de um jogo matemático, usando o Jamboard. Para acessar o vídeo, basta clicar no link que segue:
4. Relacionando os conhecimentos

Relacionando os conhecimentos
Para melhor compreender os conhecimentos aprendidos nesta unidade de estudos, assista ao vídeo que se segue, bem como leia o documento postado abaixo. Ele é de leitura obrigatória.
5. Referências
LEALDINO FILHO, P. Jogo digital educativo para o ensino de matemática. Dissertação de Mestrado, Universidade Tecnológica Federal do Paraná. Programa de Pós-graduação em Ensino de Ciência e Tecnologia: Ponta Grossa, 2013.
MAIA, D. L. ENSINAR MATEMÁTICA COM USO DE TECNOLOGIAS DIGITAIS: UM ESTUDO A PARTIR DA REPRESENTAÇÃO SOCIAL DE ESTUDANTES DE PEDAGOGIA. Dissertação de Mestrado, Mestrado Acadêmico em Educação, Universidade Estadual do Ceará: Fortaleza, 2021.