Livro didático 1 da disciplina

Neste segundo capítulo, vamos estudar as propriedades dos números reais. Este conjunto, representado pela letra R, abrangem todos os números com representação decimal, finita ou infinita, periódica ou não-periódica.

Lembrando que, os principais subconjuntos de R são

Representação	Conjunto	Elementos	Propriedades fundamentais
N	Números naturais	{0, 1, 2, 3, ...}	Conjunto criado para explicar as quantidades utilizadas para  contagem. Tem um elemento mínimo (o zero).
Z	Números inteiros	{..., -3, -2, -1, 0, 1, 2, 3, ...}	Conjunto criado para explicar os elementos representantes de saldos ou diferenças. Tem o chamando elemento oposto da adição (-x).
Q	Números racionais		Conjunto criado para explicar as frações ou partes. Tem o elemento oposto da adição e o elemento inverso da multiplicação (1/x ou  x-1), quando x for não nulo.

Nos conjunto N e Z, vamos relembrar rapidamente o conceito de divisibilidade: se existem a e b naturais não nulos, e x natural tal que ax = b, então dizemos que:

• b é divisível por a;
• b é múltiplo de a;
• a é divisor de b;
• a divide b (a | b). A notação | significa "divide".

Exemplo: os números 2 e 8. Como 2 vezes 4  = 8, e 4 é número natural, então:

• 8 é divisível por 2;
• 8 é múltiplo de 2;
• 2 é divisor de 8;
• 2 divide 8 (2 | 8). A notação | significa "divide".

Analogamente, podemos estabelecer as mesmas relações de divisibilidade em Z.

Esses conjuntos, serão estudados mais a fundo, com o devido formalismo e rigor, na disciplina de Álgebra, no sexto semestre. Aqui, vamos enunciar as propriedades elementares dos números reais, que balizarão nosso estudo daqui para frente.

Além disso, no conjunto Q, cada fração de dois inteiros pode ser expressa como número decimal finito ou dízima periódica.

Através da reta numérica, podemos representar geometricamente esse conjunto R. Observe que, entre cada número inteiro, podemos "preencher" a reta com infinitos números racionais e também irracionais.

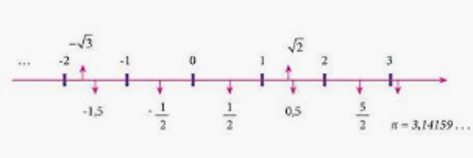
Fonte: https://brainly.com.br/tarefa/21049594

Adicionando os números irracionais (tema da próxima leitura obrigatória), temos o conjunto dos números reais. Observe o diagrama a seguir, que destaca N c Z c Q c R.

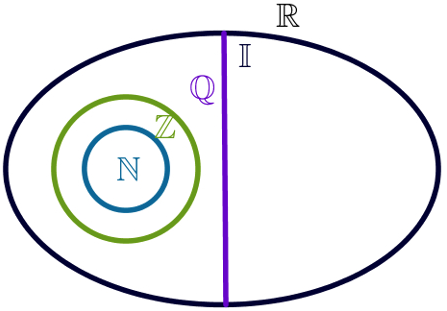
A respeito dos números reais, você vai estudar neste segundo capítulo:

• o conjunto R (junção dos racionais e irracionais);
• operações em R e propriedades (adição e multiplicação);
• definição de números irracionais, e propriedades 
• relação de ordem (maior, menor ou igual);
• intervalos reais (importantes subconjuntos de R)
• módulo ou valor absoluto