Livro didático 1 da disciplina

O conceito de conjunto em matemática é o que chamamos de conceito primitivo.

Não se define matematicamente o que vem a ser um conjunto. Temos uma concepção intuitiva do que ele se trata, e isto para nós será o suficiente. Ele simplesmente "existe" e pronto. Ponto, reta e plano, lá da geometria, também são exemplos de conceitos primitivos. A partir destas ideias comuns, desbravamos toda a matemática moderna.

De fato, esta breve introdução à extensa Teoria dos Conjuntos, que teve seu desenvolvimento no fim do século XIX e começo do século XX, leva-nos a importantes pontos da filosofia e da lógica. Temos aqui nosso primeiro contato com a linguagem eminentemente matemática, que vai no guiar de agora em diante até o final do curso.

Neste primeiro capítulo, você vai estudar:

• conjunto (noção intuitiva);
• pertinência (quando um elemento pertence ou não a um conjunto);
• inclusão (quando um conjunto é subconjunto de outro conjunto);
• operações entre conjuntos (união, intersecção e diferença);
• cardinalidade (refere-se à "quantidade de elementos de um conjunto")
• produto cartesiano (conceito fundamental para a definição posterior de relações e funções).

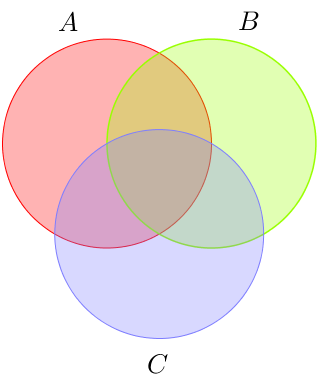
Assim sendo, vamos começar.

Neste segundo capítulo, vamos estudar as propriedades dos números reais. Este conjunto, representado pela letra R, abrangem todos os números com representação decimal, finita ou infinita, periódica ou não-periódica.

Lembrando que, os principais subconjuntos de R são

Representação	Conjunto	Elementos	Propriedades fundamentais
N	Números naturais	{0, 1, 2, 3, ...}	Conjunto criado para explicar as quantidades utilizadas para  contagem. Tem um elemento mínimo (o zero).
Z	Números inteiros	{..., -3, -2, -1, 0, 1, 2, 3, ...}	Conjunto criado para explicar os elementos representantes de saldos ou diferenças. Tem o chamando elemento oposto da adição (-x).
Q	Números racionais		Conjunto criado para explicar as frações ou partes. Tem o elemento oposto da adição e o elemento inverso da multiplicação (1/x ou  x-1), quando x for não nulo.

Nos conjunto N e Z, vamos relembrar rapidamente o conceito de divisibilidade: se existem a e b naturais não nulos, e x natural tal que ax = b, então dizemos que:

• b é divisível por a;
• b é múltiplo de a;
• a é divisor de b;
• a divide b (a | b). A notação | significa "divide".

Exemplo: os números 2 e 8. Como 2 vezes 4  = 8, e 4 é número natural, então:

• 8 é divisível por 2;
• 8 é múltiplo de 2;
• 2 é divisor de 8;
• 2 divide 8 (2 | 8). A notação | significa "divide".

Analogamente, podemos estabelecer as mesmas relações de divisibilidade em Z.

Esses conjuntos, serão estudados mais a fundo, com o devido formalismo e rigor, na disciplina de Álgebra, no sexto semestre. Aqui, vamos enunciar as propriedades elementares dos números reais, que balizarão nosso estudo daqui para frente.

Além disso, no conjunto Q, cada fração de dois inteiros pode ser expressa como número decimal finito ou dízima periódica.

Através da reta numérica, podemos representar geometricamente esse conjunto R. Observe que, entre cada número inteiro, podemos "preencher" a reta com infinitos números racionais e também irracionais.

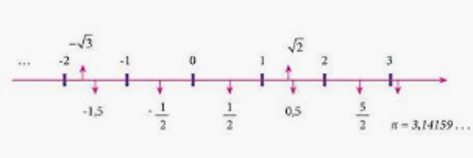
Fonte: https://brainly.com.br/tarefa/21049594

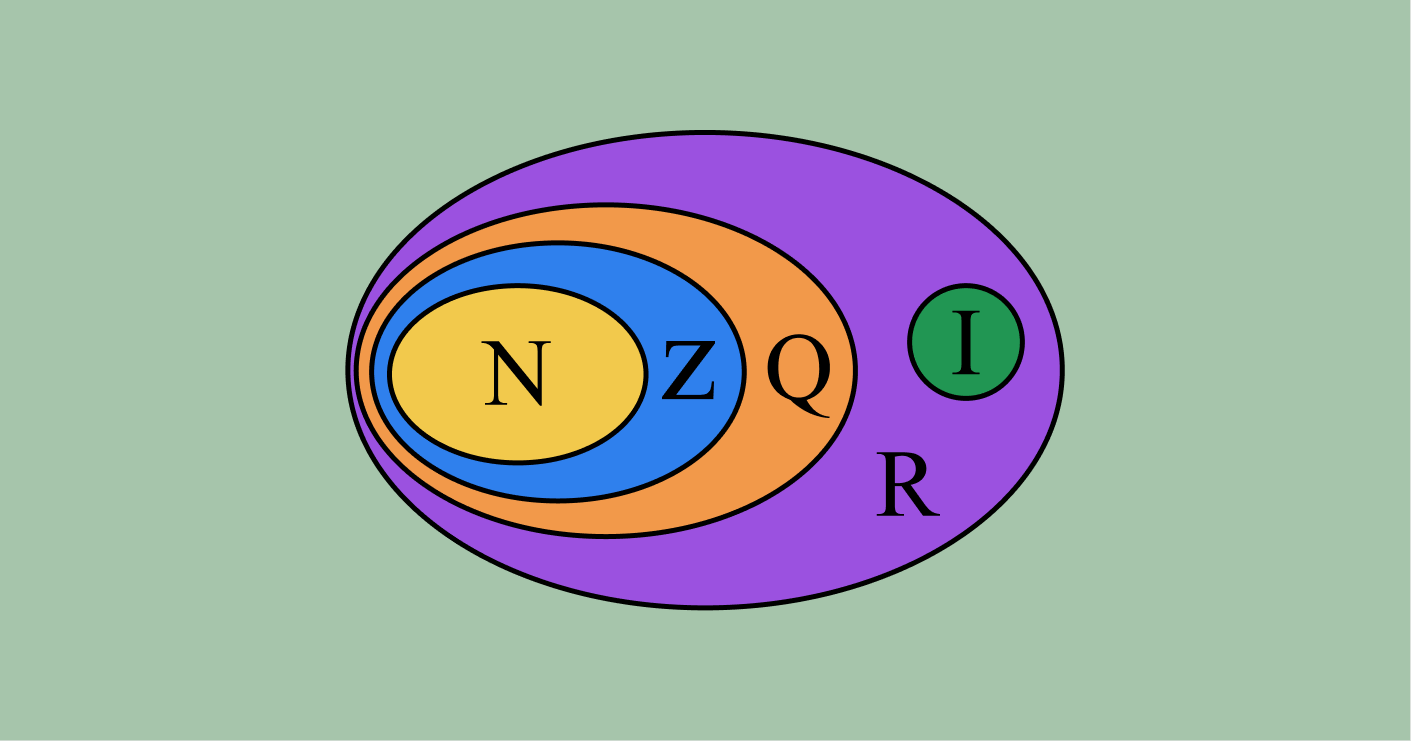
Adicionando os números irracionais (tema da próxima leitura obrigatória), temos o conjunto dos números reais. Observe o diagrama a seguir, que destaca N c Z c Q c R.

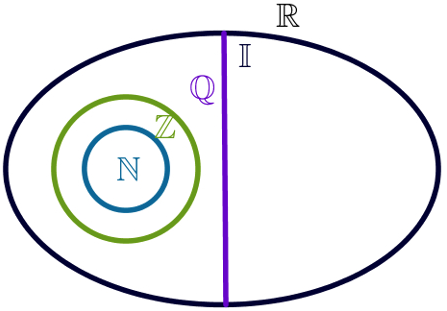
A respeito dos números reais, você vai estudar neste segundo capítulo:

• o conjunto R (junção dos racionais e irracionais);
• operações em R e propriedades (adição e multiplicação);
• definição de números irracionais, e propriedades 
• relação de ordem (maior, menor ou igual);
• intervalos reais (importantes subconjuntos de R)
• módulo ou valor absoluto