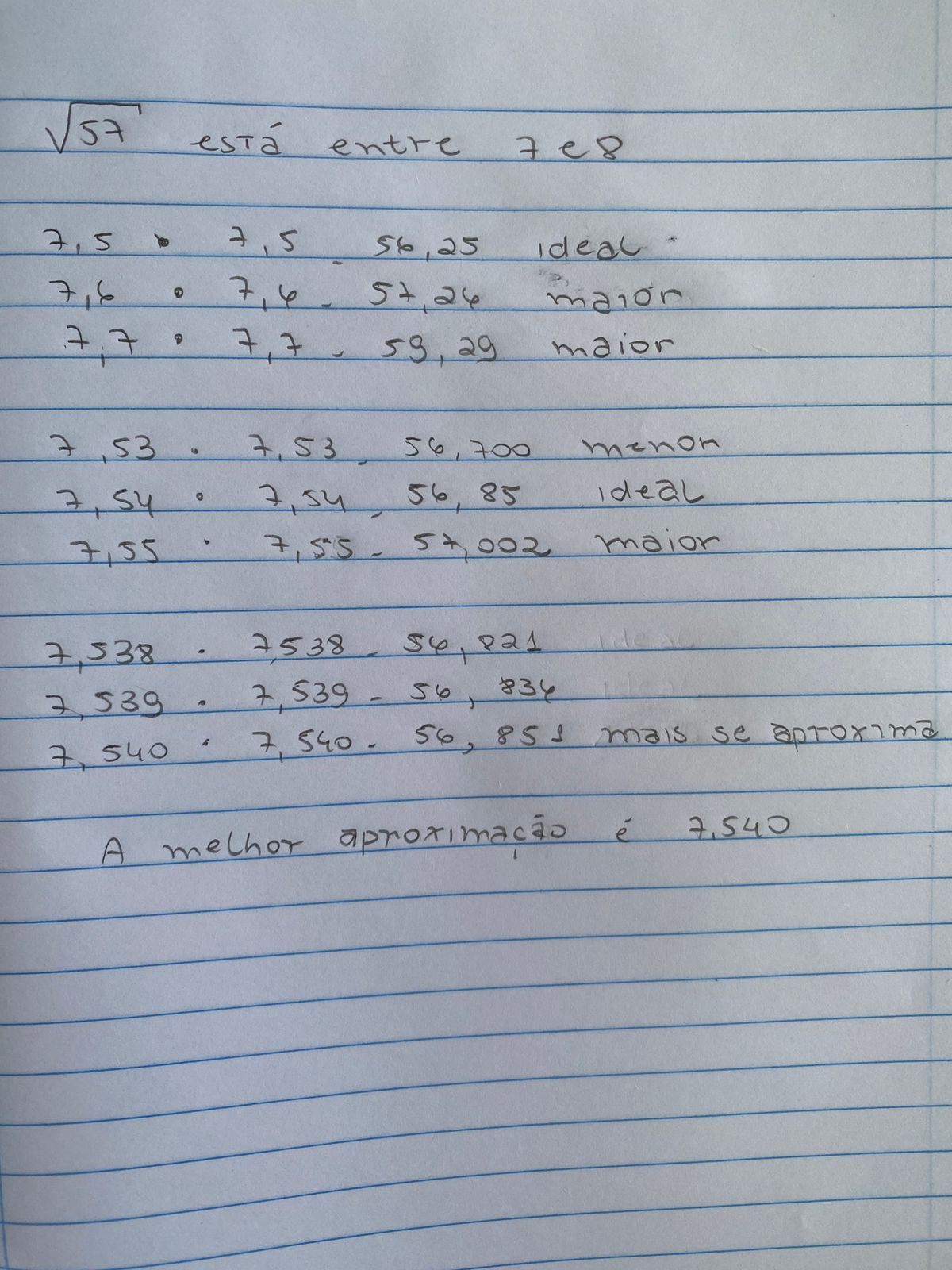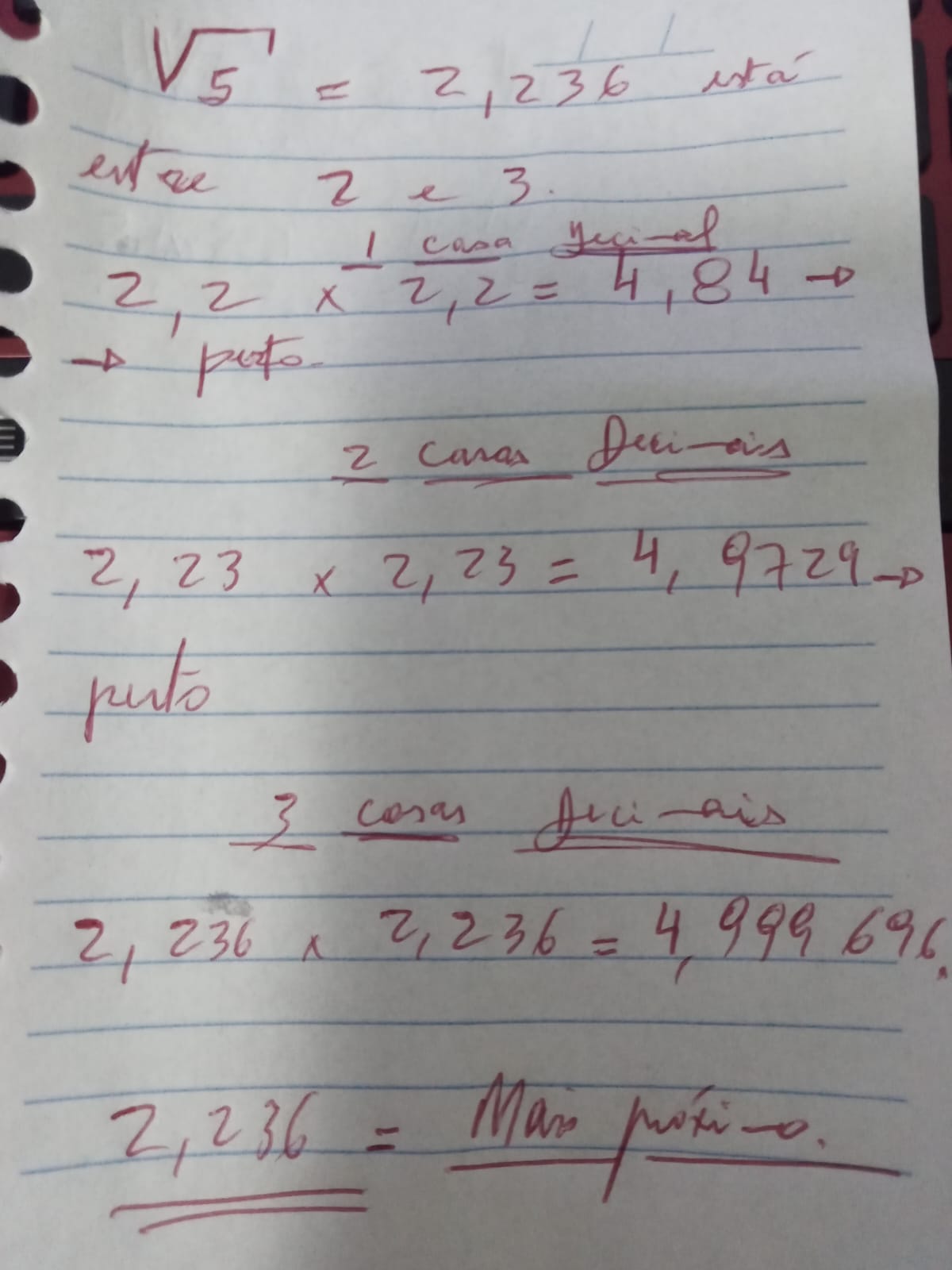O objetivo desta tarefa é obter e aproximar raízes quadradas que geram números irracionais sem utilizar a tecla "raiz quadrada" da calculadora.
Escolha um número menor que 100 que não é quadrado perfeito.
Explique uma estratégia para obter a melhor aproximação com três casas decimais utilizando uma calculadora simples que tem apenas as quatro operações aritméticas básicas (adição, subtração, multiplicação e divisão).
Por exemplo:
√2 está entre 1 e 2, pois 1 • 1 = 1 e 2 • 2 = 4 (mais perto de 1)
1,3 • 1,3 = 1,69 (então √2 é maior que 1,3)
1,5 • 1,5 = 2,25 (então √2 é menor que 1,5 e maior que 1,3, sendo mais próxima do último)
1,4 • 1,4 = 1,96 (então √2 é menor que 1,5 e maior que 1,4, sendo mais próxima do último)
1,44 • 1,44 = 2,0736 (então √2 é menor que 1,44 e maior que 1,4, sendo mais próxima do último)
1,41 • 1,41 = 1,9881 (então √2 é menor que 1,44 e maior que 1,41, sendo mais próxima do último)
1,42 • 1,42 = 2,0164 (então √2 é menor que 1,42 e maior que 1,41, sendo mais próxima do segundo)
1,414 • 1,414 = 1,999396 (então √2 é menor que 1,42 e maior que 1,414, sendo mais próxima do segundo)
1,415 • 1,415 = 2,005056 (então √2 é menor que 1,415 e maior que 1,414, sendo mais próxima do segundo)
Conclusão: Podemos afirmar que 1,414 é a melhor aproximação para √2 com três casas decimais.
Clique em “Responder” nesta postagem para apresentar sua postagem. Clique em “Responder” na postagem de um colega caso queira comentá-la.
Sua postagem deve conter:
Explicação do raciocínio para a obtenção da aproximação seguindo a solicitação do enunciado.