Livro didático 3 da disciplina
Olá,
Seja bem-vindo ao tópico 3 da nossa disciplina. Aqui você vai estudar:
Tipos de funções
- Afim e quadrática
- Exponencial e logarítmico
- Trigonométricas
| Site: | Moodle - IFSC |
| Curso: | 20.1 - Tópicos de Matemática Elementar |
| Livro: | Livro didático 3 da disciplina |
| Impresso por: | Usuário visitante |
| Data: | quarta, 17 Set 2025, 19:25 |
1. Apresentação do tópico 3
Seja bem-vindo ao livro virtual 3 da nossa disciplina. Neste livro você terá o roteiro de estudos para os temas que abrangem a Unidade Curricular, assim como terá acesso ao conjunto de materiais em pdf, cuja leitura é obrigatória para a compreensão do conteúdo.
Não se esqueça de fazer os exercícios e tarefas que estão listados ao longo de cada capítulo, no próprio material, para sua fixação e aprofundamento dos conteúdos estudados.
Os materiais deste tópico foram extraídos/adaptados de:
GIMENEZ, Carmen S. C., STARKE, Rubens. Introdução ao Cálculo 2. ed. – Florianópolis : UFSC/EAD/CED/CFM, 2010. 261p.
IEZZI, G.; MURAKAMI, C.; DOLCE, O. Fundamentos de matemática elementar: logaritmos. São Paulo: Atual, 2013. v. 2.
PINTO, M. M. F. Fundamentos de Matemática - Belo Horizonte : Editora UFMG, 2011. 141p.
Os conteúdos do tópico 3 são:
- Funções polinomiais de 1º e 2º graus
- Funções polinomiais em geral
- Funções exponenciais e logarítmicas
- Funções trigonométricas
Lembre-se
Na EaD, a disciplina de estudo é imprescindível para obter o sucesso almejado.
2. Funções polinomiais de 1º e 2º graus
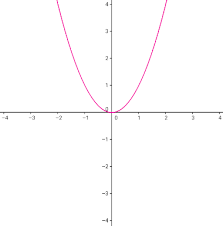
Os tipos mais comuns de funções que conhecemos são as funções polinomiais do primeiro (gráfico retilíneo) e segundo (gráfico em forma de parábola) graus.
As diversas propriedades destes dois tipos de funções, bem como as resoluções das equações correspondentes são amplamente trabalhadas no Ensino Médio, e, por vezes, também no nono ano do Ensino Fundamental.
A função polinomial do 1º grau serve de modelo para fenômenos com taxa de variação constante, ou seja, pode explicar coisas que acontecem a uma velocidade constante. Terão máximos ou mínimos apenas em casos de restrição do domínio.
Já na função quadrática a "velocidade" é variável - quando estudarmos derivadas, entenderemos que essa variação varia a uma taxa constante - e a parábola mostra graficamente o máximo/mínimo desse modelo. Podemos ter diversos exemplos de situações que recaem em expressões polinomiais do segundo grau, através das quais podemos calcular máximos e mínimos.
Portanto, vamos aqui aprofundar bem estes conceitos, além de estudar tópicos usualmente deixados de fora da nossa sala de aula, mas que podem, se bem utilizados, facilitar as resoluções e interpretações de equações polinomiais de primeiro e segundo graus.
Neste capítulo, você vai estudar:
- funções afim (gráficos e propriedades)
- funções quadráticas (gráficos e propriedades
- exercícios com situações-problema correspondentes
Leitura obrigatória
Clique aqui para ler o material sobre funções polinomiais de 1º e 2º graus.
Após a leitura obrigatória assista ao vídeo e observe na prática as funções polinomiais de 1º e 2º graus.
Na prática
Funções polinomiais de 1º e 2º graus
3. Funções polinomiais e racionais
Além das funções afim e quadráticas, que vimos no capítulo anterior, podemos ter funções polinomiais de terceiro grau, quarto grau, etc., além das funções racionais, que envolvem expressões fracionárias.
Estas funções geram gráficos pouco usuais no nosso estudo. Nem assim deixam de ser importantes para entendermos o comportamento de possíveis modelos matemáticos utilizáveis.
Leitura obrigatória
Clique aqui para ler o material sobre funções polinomiais e racionais.
Após a leitura obrigatória assista ao vídeo e observe na prática como as funções polinomiais e racionais aplicadas
Na prática
Uma explicação resumida de funções polinomiais
4. Funções exponenciais e logarítmicas
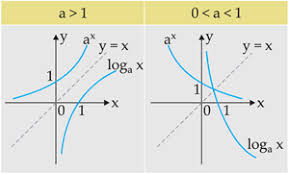
Legenda: Funções exponenciais e logarítmicas
Fonte: http://blogdoprofh.com/2017/08/25/lista-online-sobre-as-funcoes-exponencial-e-logaritmica/
O conceito de crescimento exponencial e escala logarítmica é amplamente utilizado pelos cientistas de diversas área, como física, biologia, química, sismologia, entre outros.
O pH de uma solução, bem como a magnitude de um terremoto, nada mais são que logaritmos. Suas fórmulas aparentemente complicadas nada mais são que maneiras práticas de se medir aquilo que se deseja. O nível de intensidade de uma onda sonora (decibel) é outro exemplo conhecido.
Além disso, o crescimento de uma população de bactérias, assim como a variação de massa de uma substância radioativa em um ambiente, são exemplos clássicos de fenômenos considerados exponenciais. Assim, vamos compreender um pouco mais o que esse modelo exponencial, com todas as suas peculiaridades, tem a ver com os tão temidos logaritmos.
No gráfico ao lado, temos um esboço do gráfico destas duas importantes funções na matemática. Lembrando que as funções exponenciais e logarítmicas são chamadas funções inversas uma da outra.
Neste terceiro capítulo, você vai estudar:
- exemplos de situações com comportamento exponencial
- gráfico (curva exponencial)
- logaritmos e funções logarítmicas
- modelos logarítmicos
- funções exponenciais e logarítmicas como inversas uma da outra
Leitura obrigatória
Clique aqui para ler o material sobre funções exponenciais e logarítmicas.
Após a leitura obrigatória assista ao vídeo e observe na prática como as funções exponenciais e logarítmicas são aplicadas
Na prática
Veja como ocorre a aplicação das funções exponenciais e logarítmicas
<
5. Funções trigonométricas
O último capítulo de nossa disciplina falará um pouco sobre as funções trigonométricas.
Na escola, apendemos/ensinamos as razões trigonométricas em um triângulo retângulo: seno, cosseno e tangente. Em seguida, temos a trigonometria na circunferência, em que passamos a conceber estas mesmas razões em um sistema de coordenadas cartesianas.
Estes dois temas serão abordados com mais ênfase na disciplina de Geometria Plana, que virá logo em seguida, no módulo II deste semestre. Aqui, vamos recapitular os temas centrais de trigonometria para então, podermos desbravar as funções seno, cosseno, tangente e afins.
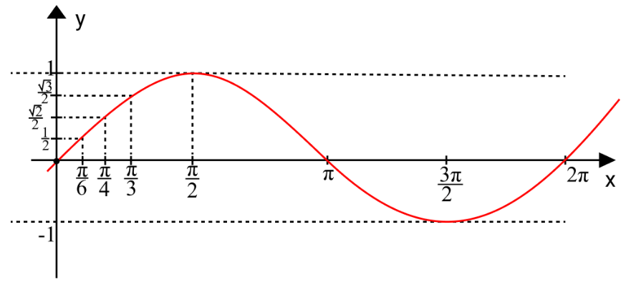
A função trigonométrica é o exemplo mais conhecido de função dita periódica.
Observe na imagem anterior que a linha do gráfico vai e volta de uma forma repetida e constante, o que mostra o caráter periódico do mesmo.
Os fenômenos com comportamento periódico (marés, batimentos cardíacos, oscilações de uma onda) podem ser modelados matematicamente através de expressões que envolvam as funções trigonométricas conhecidas (seno, cosseno, tangente e afins).
Através destas funções, podemos analisar a amplitude e periodicidade desses fenômenos. Assim sendo, vamos desbravar então mais este tipo de função.
Sendo assim, neste último capítulo da disciplina, vamos estudar:
- temas de trigonometria (arcos, medida em radianos, circunferência)
- função seno e cosseno na circunferência (gráficos)
- funções inversas de seno e cosseno (arcosseno e arcocosseno)
- função tangente e arcotangente (gráficos)
Leitura obrigatória
Clique aqui para ler o material sobre funções trigonométricas.
Após a leitura obrigatória assista ao vídeo e observe na prática como calcular as funções trigonométricas
Na prática
Calculando as funções trigonométricas